4 - Light

	Here we examine how electromagnetic vibrations can be explained within the aether model. We also take a closer look at QED and the particle/wave duality of light, the photon energy as well as electron-positron annihilation.
	Light as a Vibration of the Aether
	The Photon
	Aether, QED and the particle/wave duality of light
	Energy of a Photon
	Electron-Positron annihilation
	Light as a Vibration of the Aether
	One of the main difficulties people have with the concept of light as a vibration of the aether is the issue of transverse waves. If we assume that the aether is somewhere between a gas and a liquid, as outlined in the Aether section, then we are faced with the difficulty that gases and liquids don’t normally support transverse vibrations. However under certain conditions a liquid can support transverse waves. This has been proven by recent discoveries where it was found that supercooled liquid Helium is able to transmit transverse sound waves [1]. In other words, a state of matter where the atoms behave as a liquid but also display collective behaviour that is able to provide the restoring forces needed to support transverse oscillations. The closest we would normally come to seeing this type of behaviour is with the metal mercury. Mercury is a liquid at room temperature but because of its high surface tension it exhibits collective behaviour. A drop of mercury liquid will move about on a flat surface as a unit rather than the disordered spreading out that we see with water for example. This can be seen more readily by sprinkling powder on the surface of a mercury drop. When the drop moves all the powder particles on the surface will move in unison, illustrating that the surface of the mercury drop retains a collective movement even though it is a liquid. That is, the drop 'rolls' along the surface rather than spreading out. We will assume that the aether has properties similar to mercury or the supercooled liquid Helium. Bearing in mind that electromagnetic radiation gets generated from accelerated charges, it becomes obvious from the discussion in the Magnetism section how light would be produced in the aether scenario.      Fig 4.1  Generation of an aether wave. As the charges are accelerated in one direction and then in the opposite direction, such as occurs in a radio antenna, we would get oscillations of aether circulation around the direction of the charge movement. Somewhat like the motion of a washing machine which rotates the water in alternate directions around the axle. We must bear in mind that in our model there is a 4D component to the aether rotation so it is not just a simple rotation of aether particles around the axis. One would expect that such disturbances in the aether would be propagated away radially from the line of charge motion (Fig 4.1). We can see from the above diagram that the radiation would be primarily a transverse or shear wave.
	The Photon
	We know that visible light is usually generated by the transition of electrons from one energy state to another lower energy state. In such a case we would expect that the electrons are in some way first accelerated and then decelerated as they move from one energy orbital to another. From the previous discussion we would expect that such accelerations would produce a wave disturbance radially outwards from the line of motion of the electrons. The difference here being that the disturbance is of a short duration because the motion of the electron goes through only half a wave cycle compared to oscillating charges. However we would expect that the disturbed aether would rebound from the half wave rotation and cause a disturbance or wave rotation in the opposite direction, but of smaller magnitude. It would make sense that this motion would continue for a number of cycles, each with a diminishing amplitude, until the aether reverts back to a normal state. 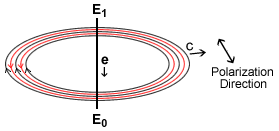     Fig 4.2  Generation of a photon. This would imply that the transition of the electron would generate a wave train that spreads out in ever expanding circles perpendicular to the line of motion of the accelerated electron, Fig 4.2. Somewhat analogous to the way a rock thrown into a pond will generate a surface wave train that moves out in ever expanding circles from the point of impact. The mechanism of generating the wave train would however be different in the two cases. This ‘wave train’ is what the standard theories would refer to as the photon. It has a finite extension consisting of several waves so that it has some properties of a particle and at the same time behaves like a wave with a specific frequency. It is also easy to see that the frequency of the wave train will be dependent on how strongly the electron is accelerated and decelerated as it moves from one energy state to another. And this will be dependent on the difference between the two energy states. This is consistent with the E = hf formula relating energy to frequency that applies to photon radiation, h being Plank's constant.
	Aether, QED and the particle/wave duality of light
	Modern science has not been able to reconcile the particle/wave duality of light. In some cases it clearly behaves as waves, such as with diffraction, and at other times as a particle. A sensitive light detector will register distinct 'clicks' or events rather than a continuous effect, which is suggestive of a particle or a quantum of light. It cannot simply be an expanding spherical compression wave in a medium as some people have suggested because several light detectors placed equidistant from the source will not fire simultaneously. Also the energy of each 'click' is constant independent of the intensity of the source, the number of 'clicks' being proportional to the intensity of the light. How then does one reconcile the two different behaviors? Physics has given up trying to understand the inner workings of light. Quantum Electrodynamics (QED), which is our best attempt at explaining the behavior of light, has a set of rules that correctly predict light intensities for various configurations but is unable to give a conceptual explanation of why it behaves as it does, [2]. We believe that the above photon model provides a plausible resolution of the particle/wave contradiction. As an example of this we will first consider the often quoted case of light scattering by two slits. When coherent light is shone through two closely spaced slits the light intensity on a screen behind it displays regularly spaced maxima and minima, Fig 4.3, rather than just a simple shadow of the slits. 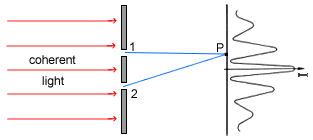      Fig 4.3  Double slit diffraction of light. The variation in light intensity can be 'explained' as a superposition of waves originating at the slit positions. That is, the intensity at P of Fig 4.3 for example can be calculated by adding the amplitudes of two waves, one originating at slit 1 going to P and the other from slit 2 going to P, with their correct phase relationship. The intensity curve is similar to what one sees when the height from two sources of water waves are combined.  This clearly displays the wavelike behavior of light. However, light detectors placed at the screen still only detect one photon or quantum of light at a time. One might suppose that the photons traveling through slit 1 somehow interact with the photons going through slit 2 to produce the maxima and minima. However this explanation is incorrect because experiments show that if the intensity of the light is reduced to such an extent that only one photon travels past the slits at any one time it still produces the same intensity variation when averaged over many photon counts. It is as if a single photon goes through both slits, interferes with itself to produce the maxima and minima. What then is a photon? If it were a particle one would expect it to be localized, so that it either goes through slit 1 or slit 2 but not both. However interference requires a superposition of waves from two different points that are coherent or in phase with one another. Without the addition from two coherent sources the whole concept of interference is meaningless. Therefore logically we have to conclude that whatever one conceives the photon to be it has to cross both slits in it's journey from the source to the screen or detectors. This means that in it's lateral extent it has to be at least as large as the slit separation. Our photon model described in the previous section fits the requirements.                  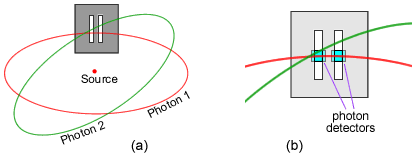Fig 4.4 Photon geometries for the double slit diffraction experiment. The photon rings cross both slits in most cases, Fig 4.4(a). The plane of the photon ring will take on many different angles. The angle being dependent on the direction of the electron motion that generates each individual photon ring as described in the previous section. Also, the photon has a short extent in the direction of travel giving us the characteristic quantum property. Our photon model also allows us to explain some other anomalies associated with the quantum nature of light. With the standard particle picture of a photon one is led to ask whether we can find out which hole or holes the photon went through in the above double slit experiment to produce interference. It has been observed experimentally however that if we placed photon detectors behind the slits, Fig 4.5, in order to try and determine which hole the individual photon went through we would lose the interference.                 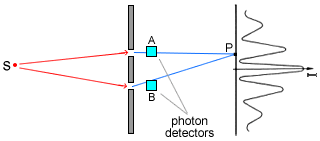Fig 4.5  Trying to detect which slit a photon goes through.  This has become one of the mysterious rules of QED theory, derived from observation, which says that if a photon, or any quantum 'particle' for that matter, has a number of possible paths it can take in order to get from A to B then we have interference between the wave amplitudes for the different paths. However if we know which path a quantum 'particle' takes we lose the interference, and the intensity or probability of observing a 'particle' is the sum of individual probabilities taken separately, see [2]. We would like to propose a simpler and more intuitive explanation for this. In the above example, Fig 4.5, if photon detector B registers a 'click' it blocks the contribution of our photon originating from slit 2, which is required for the interference to occur, so that we are left with the pattern corresponding to slit 1 alone being opened. It is also generally accepted that photon detectors A and B in Fig 4.5 do not register the same photon, that is produce simultaneous 'clicks'. This would have contributed to the standard QED picture as discussed above. This can also be understood with our photon ring model. From Fig 4.4(b) we see that the two photon detectors, A and B, will only register simultaneous 'clicks' when they both coincide with the plane of a photon ring. For the majority of photons this will not be the case. Therefore, depending to some extent on the construction of the detector, only a small portion of the photons will register simultaneous 'clicks' on both counters. It is quite conceivable that experimenters do see some coincident hits but because it occurs in only a fraction of the cases it would be natural for them to assume that these were cases where more than one photon happened to be emitted at roughly the same time. This would need to be investigated further. The second example we would like to consider here is that of a diffraction grating. Fig 4.6 shows an idealized grating consisting of regularly spaced grooves that produce maxima and minima in scattered light intensity. The standard QED explanation of this is that light from a source (S) is scattered from the raised elements of the grating, paths A,B,C,D, to produce an intensity at P that can be calculated by summing the individual amplitudes for each path A,B,C,D with the correct phases defined by the path lengths S-A-P, S-B-P, etc.                 Fig 4.6  Light scattering by a diffraction grating. Whether we get a maxima or minima at any point P will be determined by whether the individual path contributions interfere constructively or destructively. See Richard Feynman's work [2] Ch2 for a more detailed explanation. Now here is the interesting bit, it has been found experimentally that if the intensity of light is reduced to the extent that only one photon travels between S and P at any one time we still get the same maxima and minima variation when the data is averaged over many photon counts. This is the same dilemma as with double slit diffraction - how can a single photon that is supposed to be a 'particle' traverse all the different paths in order to produce interference. The only way that this result makes any sense is to assume that parts of the photon travel through all the different paths. Put another way, there must be a coherent energy disturbance that travels along path A, path B, etc, otherwise the concept of interference and the QED approach are meaningless. Again, our photon model gives us a solution to this dilemma. Fig 4.7 shows how an expanding photon ring is able to affect many of the raised groves in the grating in a coherent way.                 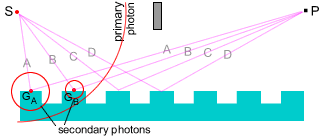Fig 4.7  Photon scattering by a diffraction grating. We are suggesting that when the photon ring arrives at the A grove point (GA) it causes electrons in the grating to oscillate in resonance. The exited electrons then in turn generate a secondary photon ring, in phase with the original photon, that then travels from GA to point P. Similarly for GB, etc, giving the correct phase relationships between the different paths. This explains how a single photon can generate the diffraction maxima and minima. Not all photon rings will have their plane positioned as shown above, some will have their planes parallel to the grating groves and will not contribute to the interference. However, on the average there will be many photon rings that cross two or more grooves contributing to the interference. This picture is not too dissimilar to the classical electromagnetic treatment of light propagation. Many of the properties of light interacting with matter, such as interference, reflection, transmission, absorption, bending of light, etc, can be explained by assuming that electromagnetic waves impinging on matter cause it's electrons to vibrate in resonance, which in turn creates secondary waves that then interfere with one another [3]. What is different about our model is that it says that a single photon can influence more than one electron. This would be analogous to an expanding ring of water surface waves, generated for example by throwing a rock in a pond, being able to influence many separate objects floating on the surface.
	Energy of a Photon
	The discussion in the previous section then leads us to re-examine the meaning of a photon's energy as given by E = hf. Is it not odd that a photon's energy should be proportional to it's frequency with no reference to the amplitude of the waves? Wave and field amplitudes normally feature in determining wave energies, so how does frequency figure in all of this? From our model of light we have that the frequency represents oscillations of the aether corresponding to variations in the magnetic field. 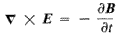If we look at the following Maxwell's equation:                          where B is the magnetic field                        E is the electric field we see that a changing magnetic field will produce an electric field at right angles to the changing B vector. The faster the magnetic field changes, ie the higher the frequency of light waves, the stronger the induced electric field. The electric field represents the force exerted on a nearby charge due in this case to a changing magnetic field. We think it is more useful to view the photon's frequency as representing the force that it can exert on a charge rather than the photon's total energy. The standard E = hf photon energy required to make an electron jump from a lower to a higher energy orbital inside an atom can be considered to represent the minimum force required to produce that jump. The corresponding energy will be given by the usual force x distance considerations, where the distance represents the length for which the force is applied. This does not mean that other parts of the photon ring cannot also affect other electrons in the same way. Only the part of the photon ring interacting with the electron will lose it's energy to the electron. This is similar to the way water waves will affect multiple objects floating on the surface. This resolves another of the paradoxes of the standard theory - the absorption of a photon through it's interaction with an electron inside an atom (the Photoelectric effect). As we have argued in the previous section, the photon has to be at least as large as the slit separation in the 2 slit photon interference experiment for the whole thing to make sense. For light this means at least ~ a millimeter in size. Even without that, it is difficult to see how a photon could be smaller than one wavelength of the light vibration constituting it, which for red light is ~ 10-6m. Therefore, we have to ask how can an electron whose motion is normally limited to atomic dimensions (~10-10m) absorb or negate a disturbance at least 104 times larger, and more likely at least 107 times larger, than the atom. This is conceptually illogical. (We note that although it is possible to create a disturbance smaller than one wavelength by superimposing a number of waves of slightly different frequency, to negate that disturbance would involve negating all the constituent waves, which leads us back to the original dilema.) This problem does not arise with our model as the electron only affects the part of the photon ring that it interacts with, it does not negate the whole photon. It only appears to do so conventionally because of the way the photon energy has been defined. The author is not aware of any experiment that clearly demonstrates that the photon is totally annihilated. Very few experiments deal with single photons, most involve light that is constituted from numerous photons. It would be difficult to determine accurately what happens to any one single photon under such conditions. Going back to the photon interference experiments described in the previous section, the photomultiplier that is used to detect photons will register a hit whenever an electron is knocked free of an atom so that it can then be detected and amplified by the instrument to register a signal. If we then assume that the probability of knocking an electron free is proportional to the intensity of the light at the detector our photon description is complete.
	Electron-Positron annihilation
	In our model the positron is the same as the electron but with aether spins reversed, see the Atoms&QM section for a more detailed discussion of this. Therefore, in an electron-positron annihilation we have the two particles both creating magnetic type aether spins in the same direction. This is because although their charges, and therefore spin directions, are normally opposite they are moving in opposite directions with the result that they will both spin the aether in the same direction around a line joining the two particles, Fig 4.8. The electron and positron will accelerate towards one another under the influence of the electrostatic force and will therefore create a rapidly increasing rate of rotation of the aether just before the collision. According to our model of photon creation outlined in the previous sections, this rotational aether disturbance should give rise to an expanding photon ring at right angles to the line joining the electron and positron, Fig 4.8.      Fig 4.8  Electron-positron annihilation. Based on this reasoning, the two photons moving in opposite directions that are normally detected with electron-positron annihilation experiments are not really two separate photons but the opposite ends of an expanding photon ring. Another interesting observation with electron-positron annihilation experiments is that in a small percentage of cases three or even more photons have been detected simultaneously. This is perfectly consistent with our photon model. We see from the photon ring geometry that if a photon is registered at a detector (eg D1 of Fig 4.8) there will always be a second event registered for a detector placed at the opposite end of the ring (detector D2). However, a third event will only be registered if the third detector is coincident with the plane of the ring (D3) and nothing if it is positioned off the plane (D4), Fig 4.8. Since the probability of the plane of the photon ring being coincident with three randomly placed detectors is small our photon model accords with observation. This also strengthens our argument that a single photon can affect more than one electron, as discussed in the previous section.
	References
	[1] Lee Y., Haard T.M., Halperin W.P., Souls J.A., “Discovery of the Acoustic Faraday effect in      Superfluid 3He-B”, Nature 400, 431-433 (July 1999) [2] Richard P. Feynman, “QED The Strange Theory of Light and Matter”, Princeton University Press,       41 William St, Princeton, New Jersey, 1985    (copies available here) [3] Feynman R.P., Leighton, R.B., Sands M., “The Feynman Lectures on Physics”, Addison-Wesley,      Vol I, Sec 30-31    (copies available here)
	Go to Top