3 - Magnetism |
Here we will examine the nature of magnetism and its formation within the context of an aether model.
Magnetism as the Flow of Aether
It is well known that Maxwell’s equations have many similarities to the
hydrodynamic equations for a fluid. This is not surprising given that the
original Maxwell’s equations were derived on the basis of a fluidic medium
(aether) [1].
It is worthwhile looking at these similarities more closely.
If we consider the general equations for fluid flow where we are only interested in describing the velocity, we get the following equations [2]:
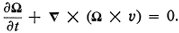
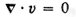
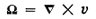
where v is the velocity of the fluid
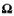is the vorticity, or circulation of the fluid
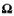is in fact a vector that points in
the direction perpendicular to the circulation and whose magnitude is
proportional to the amount of circulation, Fig 3.1(a).
If we now look at the Maxwell’s equations that describe the magnetic field we
have, for the case where there are no changing electric fields, the following:
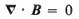
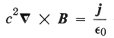
where B is the magnetic field
j
is the electric current
We can immediately see the similarities between these and the last two
equations above if we equate the velocity v with B and
vorticity 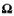with the current j.
This suggests that, at least under certain conditions, the magnetic field
represents the velocity of the aether as projected onto 3D space. That is, as
there is a 4D component to the circulation of the aether (see next item) the
aether particles would not move parallel to the 3D velocity vector above but
would move in and out of the 4th dimension, with the 3D projected velocity
being represented by v.
We can get a better idea of what is involved by considering a normal 3D vortex
such as one observes in water draining from a bathtub. If we then imagine a 2D
plane (x, y) at right angles to the vortex axis (z), the water molecules will
follow a spiral path which appears circular when projected onto the 2D plane.
However 2D flatlanders living on the plane would not see the water molecules
going in a circle, rather the molecules will appear briefly as they cross the
2D plane before disappearing again from their awareness.
We would expect something similar to occur when going from 3D to 4D space.
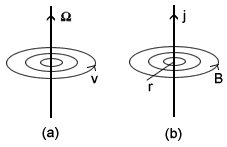Fig 3.1 Comparison
between magnetic field and fluid flow.
We can apply this idea to the case of a current carrying wire, Fig 3.1(b).
We know from experiments that the magnetic field around a current carrying wire
falls off as 1/r, where r is the distance from the wire, and is proportional to
the current.
This would imply that the projected 3D velocity of the aether also falls off as
1/r with a magnitude that is proportional to the current.
Based on the previous discussion about the similarity of the current and
the vorticity this would suggest that the moving charges that form the current
somehow create a preferential rotation of the aether around the wire.
Given that electric currents are generated by moving charges it remains to be
explained how a moving charge can create a circulating aether perpendicular to
the direction of motion.
Moving Charges and Magnetic Fields
As detailed in the previous section, a charge is considered to be a vortex of aether entering the 4th dimension, Fig 2.1 .
Lets consider the case when the charge moves in 4D.
One might expect that the aether vortex, whose axis is perpendicular to 3D
space - Fig 2.1 , would lean over behind the
direction in which the charge is being pulled, Fig 3.2.
This of course is a much simplified picture of a 4D vortex.
We would then have a net component of the vortex spin around the direction of
motion where the 4D axis meets 3D space.
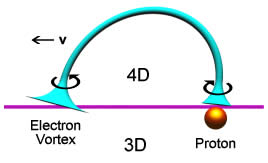Fig 3.2
Electron vortex motion in 4D.
In other words the aether flow from a charge would not be spherically symmetric
but would show a preferential rotational movement around the direction of
motion.
The magnitude of that preferential spin would depend on the speed of that
motion relative to the aether background. The faster the charge moves the more
the vortex would lean over in 4D and the greater would be the component of spin
projected onto 3D.
Motions in 4D are difficult to picture but it does make intuitive sense.
This preferential rotation of the aether around a moving charge would produce what we observe as the magnetic field, when all the individual charge contributions are summed.
This picture also neatly accounts for the fact that when a charge reverses direction of motion the magnetic field rotates in the opposite sense. That is, the vortex leans over in the opposite direction and therefore the projected spin goes from clockwise to anticlockwise or vice versa.
The idea that a charge corresponds to an aether vortex and the magnetic field to a moving aether 'fluid' is further supported by the work of R. M. Kiehn who has shown that there exists a direct mapping between the Schroedinger wave equation for a charged particle in a magnetic field and the Navier-Stokes fluid dynamic equations for vortex motion in a compressible viscous fluid. See the Atoms&QM page for more on this.
Aether, Magnetism and Relativity
Note that the above implies that the magnetic field from a charge depends on the speed of the charge relative to the aether background and not relative to the observer as standard theory suggests.
The idea that the magnetic field should depend on how fast a charge is moving
relative to the observer leads to a number of conceptual difficulties and
paradoxes. Where is the actual field in space if it depends on the observer?
By assuming that the magnetic field is dependent on the speed of the charges
relative to the aether a lot of the complexity simply disappears.
There is a logical requirement (Lorentz invariance) that the forces between
objects, such as the force between two current carrying wires, should not
depend on what the observer is doing.
In the aether model this condition will be satisfied in a natural way because
the forces surrounding moving charges will not depend on the speed of the
charges relative to the observer but relative to the aether.
Lets see if this is consistent with observation.
We can consider the situation of two parallel current carrying wires that attract each other by virtue of their magnetic fields, Fig 3.3.
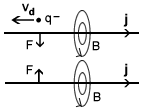Fig 3.3 The force F between two current carrying wires.
One might ask what happens if in the above example we move both the wires in
the opposite direction to the movement of the conduction electrons by an amount
equal to the drift velocity of the electrons.
In other words, the wires are moved in such a way as to make the conduction
electrons stationary, on average, with respect to the aether.
Shouldn’t this make the magnetic field disappear, contrary to experience?
On closer examination we find that moving the wires in this way causes the
positive charges of the atoms to move relative to the aether by an amount equal
and opposite to the drift velocity of the electrons (Vd in Fig 3.3).
This movement of the positive charges relative to the aether will create
exactly the same magnetic field as the conduction electrons do for the
stationary wire case.
In general, moving the wires at any speed will create a magnetic field that is
the difference between the positive and negative charge contributions.
This means that the net magnetic field will always be proportional to the
average drift velocity of the conduction electrons relative to the wire no
matter what the speed of the wires relative to the aether.
It is not too difficult to see that any neutral object, carrying any current
whatever, will behave in exactly the same way in both the aether model and the
standard theory.
Things get more interesting however when we have objects with a net charge
moving through the aether.
It is worth noting that the aether theory does not eliminate relativistic type effects. When two objects move relative to one another relativistic effects will come into play because of the finite speed of the forces, which is what relativity takes into account.
Differences Between the Aether Model and Standard Theory
It follows from the logic in the
previous section that an object with a net charge moving relative to the aether
should produce a magnetic field even for an observer traveling with the object.
Here we have a distinct difference between our aether model and standard
theory.
One might ask if this difference really exists how is it possible that this
discrepancy to standard theory has not been noticed up to now.
We believe there are two reasons for this.
Firstly, any experiments done with moving charges where the observer is
stationary with respect to the surface of the earth, will produce the same
results in the two cases.
This comes about because the aether is assumed to be stationary with respect to
the surface of the earth so that the speed of the charges relative to the
aether will be the same as the speed relative to the observer.
The second reason is that even when the observer is moving with the charges the
magnetic field predicted by the aether model is quite small for most cases that
we encounter.
To see this we consider an extreme example of a 1m diameter conducting sphere
charged to 1 million Volts. By standard electrostatic equations we can
calculate the charge on the sphere to be around 5x10-5 Coulombs.
If we now moved the sphere at 100km/hr along the surface of the earth it would
equate to a current of around 0.015 Amps.
In the aether theory this would produce a magnetic field of around 2x10-9
Teslas near the surface of the sphere, or around 10-5 the strength
of the earth’s magnetic field.
Quite easy to miss if one were not specifically looking for it!
There is however another situation where we might expect to see a much greater
effect.
All things being equal, the electrostatic forces between two charged bodies are
much greater than the equivalent magnetic forces at normal charge velocities.
One would therefore expect that the force between two charged bodies would be
affected by the movement through the aether and might be detected under normal
conditions.
There is in fact some experimental support for this idea.
Charles Morton has reported observing a variation of the force between strongly
charged bodies when they are set in motion as compared to the stationary case,
even for small speeds [3].
The force was also found to be different in front compared to the rear of
the moving charges.
This experiment, if it can be replicated, has important implications to the
current understanding of how things work.
According to standard theory the forces between charged bodies, not in motion
relative to one another, should be the same in all inertial reference frames
(frames moving at constant speeds).
The 'Morton Effect' would point to, among other things, a universal reference
frame or aether.
Further Experimental Support for the Aether Model
If we follow further the consequences
of the aether model it predicts that an observer (detector) moving
relative to a charge that is stationary with respect to the aether will not
see the usual magnetic field.
This is in disagreement with standard theory which predicts a B field whenever
an observer moves relative to charge.
Stefan Marinov carried out an experiment that is relevant to this
prediction. He used a Hall effect detector to measure the magnetic field
produced by a spinning charged disk, Fig 3.4, a variation on the Rowland
experiment.
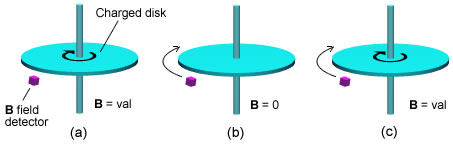
Fig 3.4 The Marinov experiment, (a)
detector is stationary and disk spins, (b) detector rotates
and disk is stationary, (c) detector and disk spin together.
He reported the following results for 3 variations of the experiment:
(a) The detector is stationary and charged disk spins. This produced a B field.
(b) The detector rotates but the charged disk is stationary. This did not
produced a B field.
(c) Both the detector and disk spin together producing the same reading as in
(a).
We will analyze these findings with the standard theory and the aether model.<
Standard Theory
(a) There is relative movement between the detector and the charges so we
expect a B field.
This agrees with
observation.
(b) There is relative movement between the detector and the charges so we
expect a B field.
This does not agree with
observation.
(c) The detector is completely stationary relative to the charges so we would
not expect a B
field to be registered.
This does not agree with
observation.
Aether Model
(a) Charges move relative to the aether so we would expect a B field.
This agrees with
observation.
(b) Charges do not move relative to the aether so we would not expect a B
field.
This agrees with
observation.
(c) Charges move relative to the aether so we would expect a B field even
though there is no
movement of the detector relative to the charges.
This agrees with
observation.
As we can see the results are in disagreement with standard theory but are completely consistent with the aether model.
References
[1] Sir Edmund Whittaker, “History of the Theories of Aether and Electricity”, Nelson LTD, N.Y. 1953
[2] Feynman RP, Leighton, RB, Sands M, “The Feynman Lectures on Physics”, Addison-Wesley, Vol II, Sec 40-42
[3] Charles R. Morton, "Velocity Alters Electric Field",
www.amasci.com/freenrg/morton1.html